Criando uma função em R para calcular a Duration de Macau...

Eu estava pensando em qual seria o primeiro tópico que abordaria em uma publicação após a elaboração da estrutura desse blog. Depois de elencar algumas possíveis opções, decidi que iria falar sobre Duration, algo relativamente básico, mas muito importante e bastante usado no mundo do mercado financeiro.

Introdução

A Duration de um ativo financeiro que constitui-se de fluxos de caixa, como um título, pode ser determinada como o tempo médio ponderado do recebimento desses fluxos; ou quando o preço de um ativo é abordado como função do rendimento, a Duration mensura a sensibilidade do preço em relação ao rendimento do título.

Dessa forma, há duas principais medidas de Duration de um título, sendo elas a Duration de Macaulay e a Duration Modificada.

Duration de Macaulay

A Duration de Macaulay, é denominada assim a partir do desenvolvimento de Frederick Macaulay, 84 anos atrás, em 1938. Ele demonstrou que a Duration de um título é uma medida mais apropriada das características temporais do que apenas o prazo até o vencimento do título, uma vez que ela incorpora o pagamento do principal na data de maturidade, o tamanho dos juros (cupons) pagos e a temporalidade dos pagamentos.

Ela indica o tempo médio (geralmente em anos) que demora para o detentor de um título receber os valores presentes dos fluxos de caixa advindos dos juros e amortizações desse título. Em termos matemáticos, tem-se a seguinte fórmula:

\[D_{Macaulay} = \frac{\sum_{t=1}^{N}{C_{t} t}}{\sum_{t=1}^{N}{C_{t}}}\]

Onde, $C_{t}$ é o fluxo de caixa trazido a valor presente no tempo t.

Portanto, a Duration de Macaulay de um título é calculada através da soma dos fluxos futuros trazidos a valor presente, ponderados pelo tempo médio de recebimento desses fluxos; divido pela soma do valor presente dos fluxos.

Sendo assim, é uma medida do tempo de vida útil de um título, considerando que os fluxos de caixa do título serão recebidos em diferentes pontos no tempo.

Duration Modificada

Já a Duration Modificada, que é resultante da derivada matemática do preço de um título, mensura a taxa percentual de variação do preço em relação ao rendimento. Ela nos permite determinar o impacto de uma variação de 1,00% na taxa de juros de interesse sobre o preço do título, sendo representada pela relação:

\[D_{Modificada} = - \frac{D_{Macaulay}}{(1 + r)}\]

Onde, $r$ é a taxa de juros de interesse.

Quanto maior for o resultado da Duration Modificada, mais sensível é o título a mudanças na taxa de juros. Como por exemplo, se a taxa de juros de interesse variar 1,00%, e o preço do título varia 1,50%; em comparação à outro ativo, onde o preço do título varia 2,75% – temos então, entre os dois, que o mais volátil é o segundo, enquanto o primeiro varia menos (sendo, nesse aspecto, um ativo mais seguro).

Criando uma função em R para calcular ambas as Durations

Após uma breve introdução sobre o que se refere Duration de Macaulay e Duration Modificada, vamos ao objetivo principal deste artigo, que é a elaboração de um código em R que retornará como output as Durations de determinado título de renda fixa, dado um fluxo de caixa (com amortizações e cupons) e uma taxa de juros de interesse.

Primeiramente, devemos carregar os pacotes que iremos utilizar na elaboração do código, onde trabalharemos com o universo de pacotes tidyverse, que conta com uma gama de pacotes com funções poderosas no tratamento de dados; e com o pacote bizdays, com diversas funções facilitadoras no tratamento de datas no padrão de dias úteis. Poderíamos utilizar library(tidyverse) e library(bizdays) para carregar os pacotes, mas incorreríamos no risco desses pacotes ainda não estarem instalados em sua máquina, precisando assim de um passo anterior: install.packages("tidyverse") e install.packages("bizdays").

Para contornar essa questão, utilizaremos o pacote pacman e com uma simples condição lógica, de forma agregada (ao invés de um por um, como seria se fizéssemos o passo anterior), checaremos se os pacotes estão instalados – caso estiverem, os carregaremos; caso contrário, os instalaremos e depois, os carregaremos, como segue:

#loading packages used
if (!require(pacman)) install.packages(pacman)
pacman::p_load(tidyverse, bizdays)

Após estarmos com os pacotes nos quais trabalharemos em cima, carregados, iremos definir como padrão o calendário de dias úteis (que desconsidera fins de semana e feriados) disponibilizado pela Anbima.

#setting anbima calendar as default
bizdays::bizdays.options$set(default.calendar = "Brazil/ANBIMA")

Para a construção do nosso problema, usaremos como base um fluxo de caixa fictício como exemplo, sendo possível o download do arquivo em .xlsx aqui. O arquivo conta com três colunas: date, referente a data de pagamento do fluxo; future_value, referente ao montante pago na data de referência; e event, explicitando se é o pagamento de um cupom ou o pagamento de uma amortização.

Para ler o arquivo dentro do R, usaremos a função read_excel() do pacote readxl, que carregamos ao chamar o universo tidyverse, como segue:

cashflow_example <- readxl::read_excel("./example_cashflow.xlsx")

Poderíamos passar outros argumentos para a função de leitura de arquivos .xlsx, mas para nosso caso não será preciso. Além disso, há dois pontos que gostaria de observar aqui: (1) como existem diversas funções com nomes iguais, porem de diferentes pacotes, gosto sempre de colocar na frente da função, a origem de seu pacote, como package::. Isto não é necessário, porém considero uma ótima prática; (2) o ./ é uma redução para referenciar o working directory do seu projeto/seu script, facilitando a nossa vida, ao invés de escrever o diretório por completo.

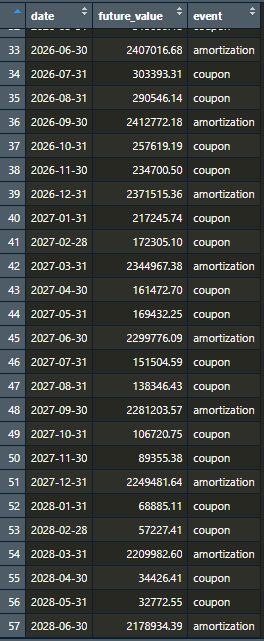
Utilizando-se da função inerte View(cashflow_example), conseguimos olhar de maneira geral o data frame que importamos do excel:

Exemplo de Fluxo de Caixa

Dessa maneira, destaca-se que o título possui 57 pagamentos de fluxo de caixa, sendo pagos cupons mensais e havendo amortizações a cada três meses, após o 18º mês, em 31/03/2025. Além disso, observa-se que o primeiro pagamento é feito em 31/10/2023 e o último em 30/06/2028, ou seja, um ativo com 65 meses de duração.

Com um simples str(cashflow_example), podemos observar que nossos dados são do tipo: date $\rightarrow$ POSIXct, future_value $\rightarrow$ numeric e event $\rightarrow$ character. Sendo assim, para uma melhor manipulação das informações, iremos alterar somente a variável date, para o formato padrão date:

cashflow_example <- readxl::read_excel(example_cashflow) |>
  dplyr::mutate(
    date = as.Date(date)
    )

Agora, depois que importamos os dados para dentro do R, que as observações iniciais foram feitas e o único tratamento necessário dos dados foi feito, iniciamos os cálculos para obtermos os valores das Durations.

initial_date <- "2022-12-26" #Sys.Date()

cashflow_example <- readxl::read_excel(example_cashflow) |>
  dplyr::mutate(
    date = as.Date(date),
    biz_days = bizdays::bizdays(from = initial_date,
                                to = date),
    time = biz_days / 252
    )

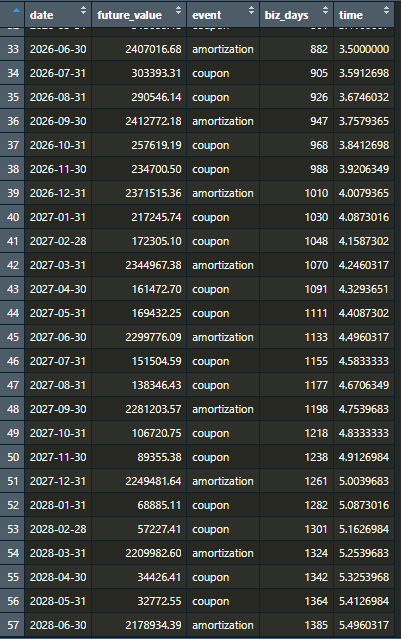
Primeiramente, criamos uma coluna biz_days que conta o número de dias úteis (com base no calendário Anbima), entre 26/12/2022 (data em que essa publicação foi escrita) e cada vértice de pagamento. Junto a isso, calculamos a variável time, que nada mais é que o número de dias úteis dividido por 252 (número padrão de dias úteis em um ano, comumente – mas não necessariamente sempre – usado para aplicações financeiras).

Exemplo de Fluxo de Caixa - Adição de Colunas

Como por exemplo, na 38ª observação, em 30/11/2026, haverá um pagamento futuro de R$234.700,50 (apenas cupom), que está a 988 dias úteis de distância da data inicial, isto é, cerca de 3,92 anos no calendário base de 252 dias.

Antes de, de fato calcular as Durations, precisamos trazer os fluxos futuros de pagamento para valor presente, a partir da seguinte expressão:

\[\text{VP}_{t} = \frac{\text{VF}_{t}}{(1 + r)^t}\]

Onde, $VP_{t}$ é o valor presente do fluxo de caixa no tempo t, $VF_{t}$ é o valor futuro do fluxo de caixa no tempo t e $r$ é a taxa de juros de interesse.

Um adendo: o valor presente possui essa fórmula uma vez que o dinheiro hoje, ceteris paribus, vale mais que o dinheiro no futuro, diferença essa alcançada pelo tempo que falta para receber esse fluxo e pela taxa de juros de interesse, que em nosso exemplo será uma taxa dada, na grandeza de 21,03%:

yield <- 0.2103

cashflow_example <- readxl::read_excel(example_cashflow) |>
  dplyr::mutate(
    date = as.Date(date),
    biz_days = bizdays::bizdays(from = initial_date,
                                to = date),
    time = biz_days / 252,
    present_value = future_value / (1 + yield) ^ time
    )

Com isso, conseguimos calcular a Duration para cada vértice de pagamento e posteriormente, calcular a Duration de Macaulay e a Duration Modificada, por meio das expressões previamente abordadas:

cashflow_example <- readxl::read_excel(example_cashflow) |>
  dplyr::mutate(
    date = as.Date(date),
    biz_days = bizdays::bizdays(from = initial_date,
                                to = date),
    time = biz_days / 252,
    present_value = future_value / (1 + yield) ^ time,
    duration_n = (present_value * time) / sum(present_value)
    )

macaulay_duration <- sum(cashflow_example$duration_n)

modified_duration <- -1 * macaulay_duration / (1 + yield)

Isto posto, observamos uma Duration de Macaulay de 3,06 anos em contraposição a uma duração do título de 5,42 anos (65 meses $\rightarrow$ duração do título, dividido por 12 meses $\rightarrow$ quantidade de meses em um ano). Além do mais, temos uma Duration Modificada de -2,53%, isto é, para uma alteração de 1,00% no yield, o preço do nosso título varia nesse montante.

Por fim, criamos uma função, em que ela recebe como input: um yield; um cashflow no formato .xlsx, conforme foi visto e uma initial_date, que caso não for informada uma data, considerará a data do dia em que o script for rodado (Sys.Date()).

Como output, a função retorna uma lista com três objetos: calculus_table, que é a tabela com as informações de date, future_value, event, biz_days, time, presente_value e duration_n; macaulay_duration, que é a Duration de Macaulay e modified_duration que é a Duration Modificada.

#duration function
duration <- function(yield, cashflow, initial_date = Sys.Date()) {
  
  cashflow_example <- readxl::read_excel(cashflow) |>
    dplyr::mutate(
      date = as.Date(date),
      biz_days = bizdays::bizdays(from = initial_date,
                                  to = date),
      time = biz_days / 252,
      present_value = future_value / (1 + yield) ^ time,
      duration_n = (present_value * time) / sum(present_value)
      )
  
  macaulay_duration <- sum(cashflow_example$duration_n)
  modified_duration <- -1 * macaulay_duration / (1 + yield)
  
  return(
    list(
      calculus_table = cashflow_example,
      macaulay_duration = macaulay_duration,
      modified_duration = modified_duration
    )
  )
  
}

Os outputs podem ser acessados ao utilizar-se do operador $, como em:

duration(yield, cashflow_example)$calculus_table,
duration(yield, cashflow_example)$macaulay_duration, ou
duration(yield, cashflow_example)$modified_duration.

Sendo que esses valores podem ser atribuídos a objetos para melhor futura manipulação.

Criando uma função em R para calcular a Duration de Macaulay e a Duration Modificada

Introdução

Duration de Macaulay

Duration Modificada

Criando uma função em R para calcular ambas as Durations